奇异值分解是一种将 矩阵 A 写成 三个矩阵乘积的分解方式： A=UDV^T。

正如同，有时我们会将一个整数写成几个整数乘积的形式一样（例如：6 = 2\times 3），将矩阵写成若干矩阵乘积的形式有助于我们研究矩阵的性质。

我们将会看到，SVD 的用途非常广泛：
– 用低维子空间拟合高维空间中的点可以对高维信息进行压缩，而 SVD 可以帮助我们找到最佳拟合子空间；
– SVD 不同于一些其它的分解算法，对于任何一个矩阵（不必须是方阵），进行 SVD 后，分解的结果 UDV^T 中，U V 均必然是正交矩阵。因此，如果 A 是方阵，其逆矩阵便是 VD^{-1}U^T

下面，我们将逐步理解 奇异值分解。
为了更好地理解 奇异值分解 的过程，我们将矩阵 A_{n\times d} 理解为 n 个 d 维空间中的点。
首先，让我们从寻找 d 维空间中的直线（一维空间）拟合这 n 个点开始。

一维拟合子空间

实际上，我们只需要寻找 d 维空间中的 一个 一维向量就可以确定一条直线

如何衡量拟合效果？

直观地，对于 d 维空间中的一个点 \textbf{v}，\textbf{v} 到 单位向量 \textbf{e} 确定的直线 的垂直距离越小，拟合效果就越好。
因此，我们尝试使得 \sum_{i}d_{i}^2（d_i 表示第 i 个点 \textbf{v}_i 到单位向量确定直线的垂直距离） 最小。
又容易知道：
|\textbf{v}_i\cdot \textbf{e}|^2+d_i^2=||\textbf{v}_i||_2^2 （投影的平方 + 垂直距离的平方 = 向量长度的平方，如下图所示）

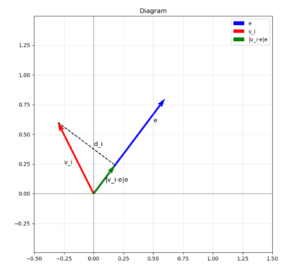
所以我们只需要最大化 \sum_{i}|\textbf{v}_i \cdot \textbf{e}|^2=||A\textbf{e}||_2^2 即可。

多维拟合子空间

回顾前文：我们将 矩阵 A_{n \times d} 看作 n 个 d 维空间中的点。
我们希望找到 d 维空间中的一个子空间，去最好地拟合这 n 个点。
实际上，我们只需要找到 子空间 的 基底 即可确定子空间。
**
引理：下面介绍一个性质，\textbf{e}_1,\textbf{e}_2,\dots,\textbf{e}_r 是 r 个相互正交的单位向量，这 r 个向量可以确定一个 r 维空间，将点 \textbf{v}_i 到这个 r 维空间的距离记为 d_i，则 d_i^2 + \sum_j{|\textbf{v}_i\cdot \textbf{e}_j|^2}=||\textbf{v}_j||_2^2
（这个性质比较直观，易于证明）

为了找到最合适的子空间， 我们尝试最小化 \sum_i{d_i^2}。
也就是最大化 \sum_{i}\sum_{j}|\textbf{v}_i\cdot \textbf{e}_j|^2=\sum_{j}||A\textbf{e}_j||_2^2

我们可以证明：利用 贪心 的策略，我们可以找到最合适的多维拟合子空间，具体过程如下：
首先找到最佳的 \textbf{e}_1：
\textbf{e}_1=\underset{\textbf{e}}{argmax}||A\textbf{e}||_2^2
然后贪心地寻找 \textbf{e}_2：
\textbf{e}_2=\underset{\textbf{e},\textbf{e}\perp \textbf{e}_1}{argmax}||A\textbf{e}||_2^2
以此类推，寻找 \textbf{e}_r 时：
\textbf{e}_r=\underset{\textbf{e},\textbf{e}\perp \textbf{e}_1,\dots \textbf{e}_{r-1}}{argmax}||A\textbf{e}||_2^2
下面我们将证明通过这种方式得到的子空间即是最佳拟合子空间（满足条件 \sum_{i}\sum_{j}|\textbf{v}_i\cdot \textbf{e}_j|^2=\sum_{j}||A\textbf{e}_j||_2^2 最大）：
数学归纳法： 根据定义，最佳一维子空间的基显然是 \textbf{e}_1
不妨假设 最佳拟合 k 维子空间由 \textbf{e}_1,\dots,\textbf{e}_k 张成的，则必有 \sum_{j=1}^{k}||A\textbf{e}_j||_2^2 （n 个 d 维空间中的点到 k 维子空间的投影的长度平方之和）最大。

讨论最佳拟合（k + 1）维子空间，不妨假设存在正交单位基底 \textbf{m}_1,\dots,\textbf{m}_{k+1}，则必然存在 LinearCombination[\textbf{m}_j(1\le j\le k+1)] ，其垂直于 \textbf{e}_1, \textbf{e}_2,\dots,\textbf{e}_{k} 张成的空间。

针对某个线性组合，在保证 \textbf{m}_1,\dots,\textbf{m}_{k+1} 张成的空间不变的前提下，选择一个完全垂直于 \textbf{e}_1, \textbf{e}_2,\dots,\textbf{e}_{k} 的基 （不妨假设为\textbf{n}_1）（对原本的基做了一个旋转）。

此时，我们会有 \sum_{j=2}^{k+1}||A\textbf{n}_j||_2^2 \le \sum_{j=1}^{k}||A\textbf{e}_j||_2^2 ，并且 ||A\textbf{n}_1||_2^2\le ||A\textbf{e}_{k+1}||_2^2
很明显，将上面两个不等式相加，我们可以得到最佳拟合 k 维子空间由 \textbf{e}_1,\dots,\textbf{e}_{k+1} 张成的，完成数学归纳法。

奇异值与奇异向量

定义矩阵的奇异值：
\delta_i(A)=||A\textbf{e}_i||_2 ，不难发现，奇异值的大小是单调递减的。

右奇异向量为：
\textbf{e}_1,\dots,\textbf{e}_{r}

实际上，右奇异向量均为 A^TA 的特征向量，下面让我们证明这个结论

我们的 \textbf{e}_1 是通过 \textbf{e}_1=\underset{\textbf{e}}{argmax}||A\textbf{e}||_2^2 得到的，也就是在限制 \textbf{e}^T\textbf{e}=1 的条件下，求函数 f(\textbf{e})=\textbf{e}^TA^TA\textbf{e} 的极大值点。

这是非常经典的问题，我们可以借助 拉格朗日 方法求解：

设 g(\textbf{e},\lambda)=\textbf{e}^TA^TA\textbf{e}+\lambda (\textbf{e}^T\textbf{e} – 1)
对两个自变量分别求偏导可得
2A^TA\textbf{e}+2\lambda \textbf{e},\space \textbf{e}^T\textbf{e} – 1
让我们回忆 f(\textbf{e}) 的意义，它表示的是 n 个 d 维空间中的点在 单位向量 \textbf{e} 上投影的长度的平方和，由于 A 是固定的，从直觉上来讲， f(\textbf{e}) 是存在极大值的，且极大值点满足上面两个偏导均为 0，由此，我们可以得到 A^TA\textbf{e}=-\lambda \textbf{e} ，显然方程的解是 A^TA 的特征向量。

我们完全可以用类似的方法得到所有右奇异向量均为 A^TA 的特征向量。

接下来定义左奇异向量：
\textbf{u}_i=\frac{A\textbf{e}_i}{\delta_i(A)}
显然有 \textbf{u}_i 之间相互正交：
\textbf{u}_j^T\textbf{u}_i=\frac{\textbf{e}_j^TA^TA\textbf{e}_i}{\delta_i \delta j} 由于 \textbf{e}_i 是 A^TA 的特征向量可以化为 \lambda_i\textbf{e}_i ，显然有 \textbf{u}_j^T\textbf{u}_i=0 。