本文主要介绍 SDE 求 Reverse 的一些理论，在扩散模型理论中应用十分广泛，与常规微分方程的 Reverse 不同，SDE 涉及到概率的概念，求解难度远远大于常规微分方程。

常规微分方程

一个普遍的形式是 dx = f(x,t)dt，写成离散化形式：x_{t+\Delta t}-x_t=f(x_t,t)\Delta t ，求 Reserve 实际上目的在于找到函数 g(t) 满足 对于任意的 x_{t+\Delta t}， g(t)=x_{t+\Delta t}时 ，必有 g(t + \Delta t)=x_t 。

简单来说，原本的 x_t 经过 \Delta t 时间后，变为 x_{t + \Delta t} ，而 g(t) 相反。
我们可以在下面的图像中得到一个直观地理解：

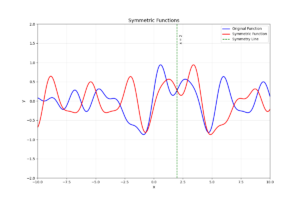
观察图中的虚线附近，蓝色线的斜率大于零，红色线的斜率小于零，而且两个函数关于虚线（x=2）对称。
蓝色线以怎样的趋势变化到 x=2 处，红色线从 x=2 处开始就以完全相反的趋势恢复。
对应到扩散模型中，我们希望找到加噪过程的一个逆过程，将所加噪声的影响消除。

SDE

下面讨论如何求解 SDE，我将以扩散模型加噪的 SDE 作为例子：
d\textbf{x}=f_{t}(\textbf{x},t)dt+g_t(\textbf{x},t)d\mathbf{\omega}
与常规微分方程的最本质不同在于 随机项的引入，使得直接将导数求相反数不再适用。我们将引入概率论的相关工具。

首先，同样将微分方程写成离散形式：
\textbf{x}_{t+\Delta t}-\textbf{x}_t=f_{t}(\textbf{x}_t,t)\Delta t+g_t(\textbf{x},t)\sqrt{\Delta t}\epsilon
（这里运用到了 维纳过程 相关的结论，\omega_{s}-\omega_{t}\sim \mathcal{N}(0, (s-t)\textbf{I})）
将离散形式下的公式用概率的语言描述：
p_t(\textbf{x}_{t+\Delta t}-\textbf{x}_{t})\sim \mathcal{N}(f_{t}(\textbf{x}_t,t)\Delta t, g_t^2(\textbf{x},t)\Delta t)
表明 在时间 t 下，\Delta t 时间后，\textbf{x} 的变化量满足如上所示的正态分布。

所以我们将会得到如下的条件概率：
p_t(\textbf{x}_{t+\Delta t}|\textbf{x}_t)\sim \mathcal{N}(f_{t}(\textbf{x}_t,t)\Delta t + \textbf{x}_t, g_t^2(\textbf{x},t)\Delta t)

忽略正态分布的归一化常数后，有：
p_t(\textbf{x}_{t+\Delta t}|\textbf{x}_t) \propto exp[-\frac{||\textbf{x}_{t+\Delta t}-(f_t(\textbf{x}_t,t)\Delta t + \textbf{x}_t)||_2^2}{2g_t^2(\textbf{x},t)\Delta t}]
两边同时取对数，可得
log[p_t(\textbf{x}_{t+\Delta t}|\textbf{x}_t)]\propto -\frac{||\textbf{x}_{t+\Delta t}-(f_t(\textbf{x}_t,t)\Delta t + \textbf{x}_t)||_2^2}{2g_t^2(\textbf{x},t)\Delta t}

由于 p_t(\textbf{x}_{t+\Delta t}|\textbf{x}_t)p_{t}(\textbf{x}_{t})=q_{t+\Delta t}(\textbf{x}_{t}|\textbf{x}_{t + \Delta t})p_{t + \Delta t}(\textbf{x}_{t +\Delta t}) ，这个等式可以根据现实意义很容易地得到，其中 p_t(\textbf{x}_{t+\Delta t}|\textbf{x}_t) 表示的是 时间 t 为 \textbf{x}_t 的前提下，时间 \Delta t + t 下为 \textbf{x}_{t+\Delta t} 的概率，q_{t+\Delta t}(\textbf{x}_{t}|\textbf{x}_{t + \Delta t}) 表示的是时间 t + \Delta t 为 \textbf{x}_{t + \Delta t} 的前提下，逆推时间 t 为 \textbf{x}_t 的概率，我为了更好的区分，使用字母 q 表示。

由于等式两边都表示的是时间 t 为 \textbf{x}_t ，且时间 t + \Delta t 为 \textbf{x}_{t+\Delta t} 的概率，所以等式显然成立。
再在两边同时取对数，可得：

log[p_t(\textbf{x}_{t+\Delta t}|\textbf{x}_t)]=log[q_{t+\Delta t}(\textbf{x}_{t}|\textbf{x}_{t + \Delta t})]+log[p_{t + \Delta t}(\textbf{x}_{t +\Delta t})]-log[p_{t}(\textbf{x}_{t})]

观察 log[p_{t + \Delta t}(\textbf{x}_{t +\Delta t})] ，其是一个关于时间 t 和 向量 \textbf{x}_{t + \Delta t} 的函数，我们知道 \Delta t 很小，因此我们可以用一阶近似来得到 log[p_{t + \Delta t}(\textbf{x}_{t +\Delta t})] 的近似值，如下：
log[p_{t + \Delta t}(\textbf{x}_{t +\Delta t})]\approx log[p_{t}(\textbf{x}_{t })] + \nabla_{t}log[p_{t}(\textbf{x}_{t })]\cdot \Delta t + \nabla_{\textbf{x}_t}log[p_{t}(\textbf{x}_{t })] (\textbf{x}_{t+\Delta t}-\textbf{x}_{t})
代入上式：

log[p_t(\textbf{x}_{t+\Delta t}|\textbf{x}_t)]=log[q_{t+\Delta t}(\textbf{x}_{t}|\textbf{x}_{t + \Delta t})] +\nabla_{\textbf{x}_t}log[p_{t}(\textbf{x}_{t })] (\textbf{x}_{t+\Delta t}-\textbf{x}_{t}) + \nabla_{t}log[p_{t}(\textbf{x}_{t })]\cdot \Delta t

很容易得到：

log[q_{t+\Delta t}(\textbf{x}_{t}|\textbf{x}_{t + \Delta t})]\propto -\frac{||\textbf{x}_{t+\Delta t}-(f_t(\textbf{x}_t,t)\Delta t + \textbf{x}_t)||_2^2}{2g_t^2(\textbf{x},t)\Delta t}-(\nabla_{\textbf{x}_t}log[p_{t}(\textbf{x}_{t })] (\textbf{x}_{t+\Delta t}-\textbf{x}_{t} – f_t(\textbf{x}_t,t)\Delta t) – f_t(\textbf{x}_t,t)\Delta t \nabla_{\textbf{x}_t}log[p_{t}(\textbf{x}_{t })] + \nabla_{t}log[p_{t}(\textbf{x}_{t })] \cdot \Delta t)
再做化简：

log[q_{t+\Delta t}(\textbf{x}_{t}|\textbf{x}_{t + \Delta t})]\propto -\frac{||\textbf{x}_{t+\Delta t}-(f_t(\textbf{x}_t,t)\Delta t + \textbf{x}_t)||_2^2+2g_t^2(\textbf{x},t)\Delta t(\nabla_{\textbf{x}_t}log[p_{t}(\textbf{x}_{t })] (\textbf{x}_{t+\Delta t}-\textbf{x}_{t} – f_t(\textbf{x}_t,t)\Delta t)}{2g_t^2(\textbf{x},t)\Delta t} + O(\Delta t)

进行一次配方法简化上式
这里用到了一点向量点积配方的相关技巧，让我们首先介绍这个技巧：
<\textbf{a},\textbf{a}>=<\textbf{a}-\textbf{x},\textbf{a}-\textbf{x}>+<\textbf{x},\textbf{x}>+2<\textbf{x},\textbf{a}-\textbf{x}>
这是类似于标量的配方法的。

log[q_{t+\Delta t}(\textbf{x}_{t}|\textbf{x}_{t + \Delta t})]\propto -\frac{||\textbf{x}_{t+\Delta t}-(f_t(\textbf{x}_t,t)\Delta t + \textbf{x}_t)+g_t^2(\textbf{x},t)\Delta t(\nabla_{\textbf{x}_t}log[p_{t}(\textbf{x}_{t })]||_2^2}{2g_t^2(\textbf{x},t)\Delta t} + O(\Delta t)

故 q_{t+\Delta t}(\textbf{x}_{t}|\textbf{x}_{t + \Delta t})\sim \mathcal{N}((-f_t(\textbf{x}_t,t)\Delta t + \textbf{x}_{t +\Delta t})+g_t^2(\textbf{x},t)\Delta t(\nabla_{\textbf{x}_t}log[p_{t}(\textbf{x}_{t })],g_t^2(\textbf{x},t)\Delta t\textbf{I})