Momentum Contrast for Unsupervised Visual Representation Learning

• 对比学习：将一系列元素通过网络（特征提取函数 f ），得到特征表达。我们希望相似的元素的特征在特征空间中距离更近，而不相似的元素的特征在特征空间距离更远。如果我们学到了一个特征提取函数 f 可以很好地满足这个要求，那么这个 f 在一定程度上可以提取出一张图片区别于其他图片的特征（一个很好的特征）。

代理任务（Pretext Task） – instance discrimination：
每张图片自成一类，由原图增广得来的图片是正样本，其他皆为负样本。
比如 一共 n 张图片 x_1,x_2,\dots,x_n ，对 其中一张图片 x_1 做数据增强得到 x_{11},x_{12}，我们可以将 x_{11} 当作锚点 （anchor），将 x_{12} 当作正样本，x_2,\dots,x_n 当作负样本。
从而构建这样一个任务，将 x_{11}, x_{12}, x_2, \dots, x_n 通过 Encoder 获得特征向量 f_{11}, f_{12}, f_2, \dots, f_n 。然后可以运用常见的对比学习的损失函数衡量 特征向量 的 好坏（f_{11} 与 f_{12} 相似程度比较大， f_{11} 与 f_2, f_3,\dots,f_n 相似程度较低——Better）。

MoCo是第一个在多个视觉任务上，无监督学习表现得比有监督学习好的模型。

MoCo的主要贡献在于，Momentum Encoder。

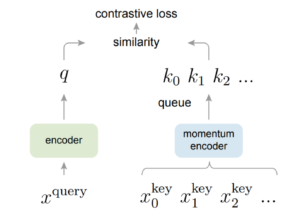
框架

上图中的 x^{query} 相当于我们之前提到的 x_{11} ，x_{i}^{key} 相当于 x_{12}, x_2,\dots,x_n 。Moco 用到了两个 编码器。

作者将所有对比学习问题总结为 字典查询问题。他可以看作拿着 x^{query} ，在 字典 {x_0^{key}, x_1^{key}, x_2^{key},\dots} 中匹配（利用我们最开始提到的符号可以表述为 拿着 x_{1} 做数据增强得到的 x_{11} ，在 x_{12}, x_2, \dots,x_n 中找到同样由 x_1 数据增强（因此具有相同语义信息）的 x_{12}）。其实，这个总结我个人感觉不是很恰当。

总体来说，作者认为 要想取得好的效果需要满足：字典很大、字典里的特征向量处在同一个特征空间中（一致）。

这不难理解，字典越大，提供的特征信息也就越丰富，对比的效果也就越好；但是字典里的特征如果不”一致“的话，对比损失也就失去了意义。

Moco 中使用两个编码器（不共享参数），用一个队列储存所有的 k_i （即 x_i^{key} 的特征）。

算法流程：
首先，将 x^{query}，x_{i}^{key} 通过各自的编码器获得特征向量 （如上图所示）。
然后，计算特征之间的相似程度并带入对比损失公式计算。
进行梯度反传更新编码器的参数。

值得注意的是，我们用队列储存 k_0, k_1, \dots ，这里，我们会将 momentum encoder 编码的向量复制一份放入队列中，然后我们利用队列中的 k_i 参与损失函数的计算。这里会有一个梯度截断。

因此，我们无法直接反传更新 momentum encoder 的编码器，作者提出以一种动量的方式更新编码器参数。

Momentum Encoder：

{\theta}_k = m{\theta}_{k – 1} + (1 – m){\theta}_q
这样，我们就不需要反传更新参数了。

m 通常取得比较大，所以 {\theta}_k 更新得比较慢，使得队列中的 key 来自相差不大的编码器。如果key来自很不同的编码器的话，那么 key 处在很不同的语义空间内，让正样本相互靠近，负样本相互远离的操作也就没有了意义。

为什么要使用队列呢？ 首先，我们可以存储过去的 Momentum Encoder 生成的特征向量，所以进行字典匹配的时候，我们是在更多的特征向量之间进行了匹配。同时，队列先进先出的特性使得当队列达到足够的长度后，再插入新的元素时，会先将最古老的元素弹出队列，最古老的元素是最古老的编码器得到了，与现在的编码器偏差是最大的，先弹出是合理的。

损失函数

• InfoNCE：
  \text{InfoNCE Loss} = -\frac{1}{N} \sum_{i=1}^N \log \left( \frac{\exp \left( \frac{q_i \cdot k_{i+}}{\tau} \right)}{\sum_{j=1}^N \exp \left( \frac{q_i \cdot k_{j-}}{\tau} \right)} \right)
  其中，\tau 为温度系数，用来控制形状。 q_i 是 query，k_{i+} 是正样本，k_{j-} 是负样本。(\cdot) 代表内积操作。
  显然这个损失函数能满足我们希望的大小关系（不难分析）。
  \tau 越大，\frac{1}{\tau} 越小，softmax 之前的值越平均。
  反之，softmax 之前的值差距越大（尖峰），导致损失函数关注极端情况。